The Time Value of Money (TVM) is a fundamental concept in finance that plays a crucial role in various financial decisions. It is a concept that recognizes the idea that a sum of money has a different value today compared to its value in the future. Understanding the time value of money is essential for making informed financial decisions, and it serves as the foundation for many financial theories and calculations. In this article, we will explore what the time value of money is, why it is important, and delve into real-world applications with practical examples.
What is the Time Value of Money?
At its core, the time value of money is based on the principle that a dollar today is worth more than a dollar tomorrow. This is because money has the potential to earn returns over time, and therefore, a certain amount of money today can grow into a larger sum in the future.
The time value of money is influenced by two key factors: interest rates and the concept of compounding. Interest rates represent the return on investment or the cost of borrowing money. Compounding refers to the process where the interest earned on an investment, or the interest charged on a loan, is added to the principal amount, creating a new, larger base for future interest calculations.
The Importance of the Time Value of Money
Understanding the time value of money is crucial for several reasons:
- Informed Decision Making: Financial decisions often involve comparing cash flows that occur at different points in time. Whether it's deciding between investment opportunities, evaluating loan options, or planning for retirement, the time value of money provides a framework for making informed choices.
- Risk and Uncertainty: The future is inherently uncertain, and the time value of money helps account for this uncertainty. By discounting future cash flows to their present value, individuals and businesses can better assess the potential risks associated with their financial decisions.
- Investment Planning: Investors use the time value of money to assess the attractiveness of investment opportunities. By understanding the present value of expected future returns, investors can determine the profitability of an investment and compare it to alternative options.
Real-World Applications
Now let's explore some real-world applications of the time value of money, along with practical examples.
Investment Valuation
One of the most common applications of the time value of money is in the valuation of investments. Whether you are considering stocks, bonds, real estate, or any other investment, understanding the present value of future cash flows is essential.
Suppose you are considering an investment that promises to pay $1,000 one year from today. If the prevailing interest rate is 5%, the present value of that future $1,000 can be calculated as follows:
Where:
- PV is the present value
- FV is the future value ($1,000)
- r is the interest rate (5%)
So, the present value of $1,000 to be received one year from today at a 5% interest rate is approximately $952.38 in todays dollars.
Loan Amortization
The time value of money is also integral in understanding loan amortization. When individuals take out loans, such as mortgages or car loans, they repay the borrowed amount over time. The interest paid on the loan is a reflection of the time value of money.
Consider a $10,000 loan with a 5% annual interest rate to be repaid over three years. Using the formula for calculating loan payments:
Where:
- PMT is the monthly payment
- P is the principal amount of the loan ($10,000)
- r is the monthly interest rate (5% / 12)
- n is the total number of payments (3 years * 12 months)

After calculation, the monthly payment (PMT) would be approximately $299.71. Understanding loan amortization helps borrowers comprehend how much of their monthly payments go towards interest and how much towards the principal.
Retirement Planning
The time value of money is a critical factor in retirement planning. Individuals need to estimate the amount of money they should save today to ensure a comfortable retirement in the future.
Suppose you want to retire in 30 years and estimate that you will need $1 million to maintain your desired lifestyle. Assuming an annual return on your investments of 7%, you can use the future value formula:
Where:
- FV is the future value ($1 million)
- PV is the present value (the amount you need to save today)
- r is the annual interest rate (7%)
- n is the number of years (30)
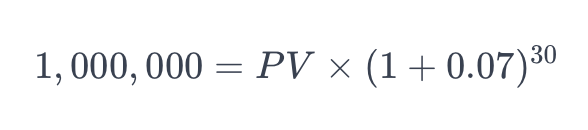
Solving for PV:
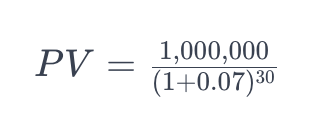
After calculation, the present value (PV) would be approximately $141,864.37. This means you would need to save around $141,864.37 today to have $1 million in 30 years, assuming a 7% annual return on your investments. This is a fundamental concept when planning for retirement.
The time value of money is a fundamental concept that underpins various financial decisions. Whether you're making investment choices, managing loans, or planning for retirement, understanding the time value of money is essential for making sound financial decisions. The time value of money is a versatile tool that empowers individuals and businesses to navigate the complex landscape of finance with confidence. By incorporating the time value of money into financial decision-making, individuals can optimize their resources, manage risk, and ultimately work towards achieving their financial goals.



